Background

In this project, I explore various applications of morphing. I morph my face into the face of Magnus Carlen, the world chess champion. Then, I use a dataset of Danish faces and compute the average face of the population, morphing the average into my face and vice versa. Finally, I use morphing to change the gender of my face for the bells & whistles portion.

Part 1: Defining Correspondences

In order to morph my face into Magnus’s, I first defined correspondence points between the two images using this tool: Correspondence Points Tool. Then, I created a triangular mesh for the two images using Delaunay triangulation, which ensured that the triangles were not too skinny. The triangulation was constructed on the average of the two correspondence points sets to avoid triangle deformation

Part 2: Computing the “Mid-way Face”

To get an idea of how to construct a sequence that morphs my face into Magnus’s, I computed the mid-way face first, which is the average combination of my face with Magnus’s. This is the face that should appear in the middle of the morphing sequence. From the previous part, I had the average shape (i.e. the average of the two correspondence points sets). To construct the midway face, I first warped my face into the average shape and Magnus’s face into the average shape. Then, I cross-dissolved the two warped images by averaging the pixel values between them. For the warping procedure, we want to warp each triangle in the source shape to its corresponding triangle in the target shape, so for each pair of corresponding triangles, we find the inverse affine transformation matrix that maps the target triangle to the source triangle. Then, to find the color of each pixel inside the target triangle, we apply this inverse affine transformation to find its location in the source triangle and interpolate among the source pixels to find the color of the target pixel. I used nearest neighbor interpolation because it ran the fastest and produced good results.

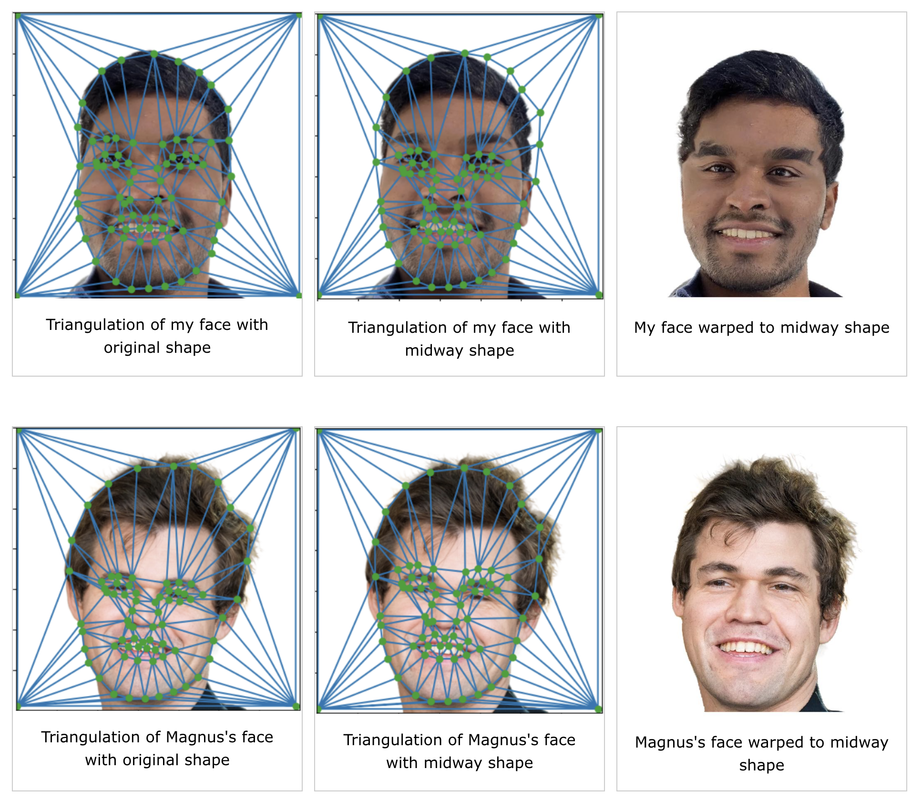
Part 3: The Morph Sequence

Now that we have an idea of how to morph between the two faces, to produce a gradual sequence that morphs between my face and Magnus’s, we simply need to vary the parameters of the morph and apply the same procedure we used in Part 2. Namely, the 2 parameters we’re concerned with are warp_frac (controls how much of my face shape is warped into Magnus’s face shape) and dissolve_frac (controls how much my face colors are changed into Magnus’s face colors). For the midway face, both of these parameters were 0.5 because we wanted an equal contribution from both faces. To produce a morph sequence, we vary these parameters from 0 to 1 and create 50 frames of gradual morphing from my face to Magnus’s. For each frame, I compute the shape to warp to as (1-warp_frac)*theo_pts + warp_frac*magnus_pts and warp both faces to this shape. Then, I cross-dissolve by computing a weighted average of the pixel values of these warped images, i.e. (1-dissolve_frac)*warped_theo + dissolve_frac*warped_magnus. The morph sequence can be seen as a GIF below

Part 4: The “Mean Face” of a Population

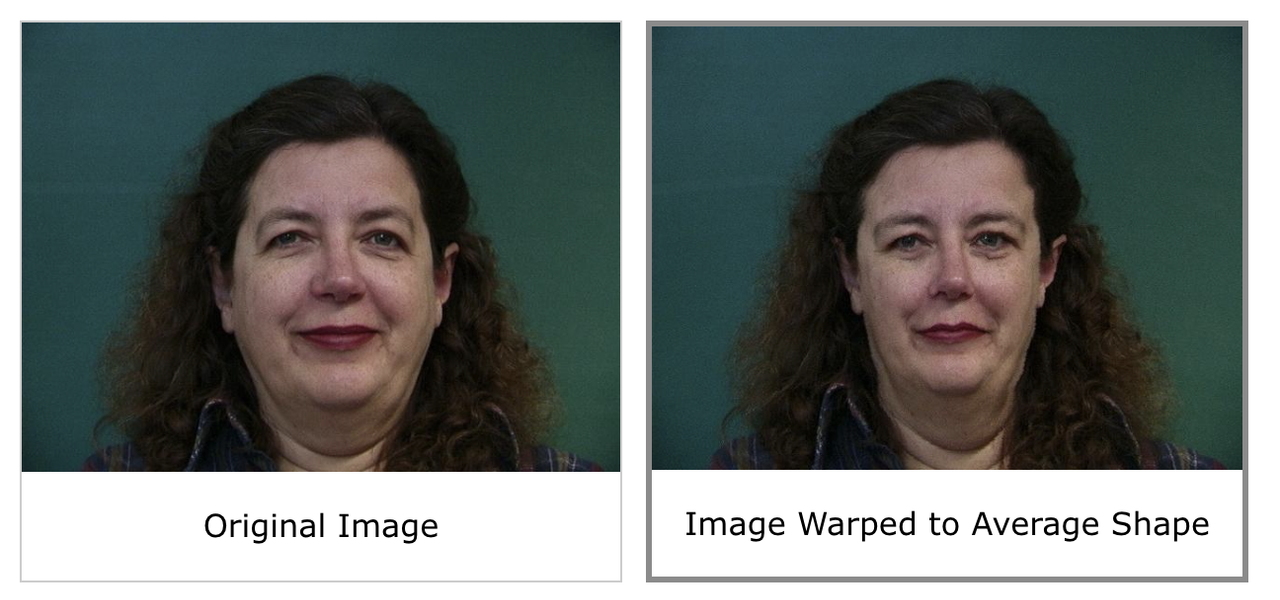
I also computed the mean face of a subset of the Danes dataset by first finding the average face shape (averaging the face vectors), warping each image to the average shape, and finally averaging the pixels of these warped images. The subset I used was the frontal face, neutral expession subset. I used the annotated face shapes provided in the dataset but added additional points to each shape corresponding to the corners of each image. The average face can be seen below. Since most of the dataset contained male faces, it makes sense that the average face also looks male.

Here are the faces of the population morphed to the average shape with some specific examples

I took another picture of my face to match the pattern in the Danes dataset, full frontal and neutral expression. Then, I morphed my face into the average Danes shape and the average Danes face into my face shape, the results of which can be seen below

Part 5: Caricatures - Extrapolating from the Mean

To produce a caricature of myself, I extrapolated from the population mean found in the previous part. If a is the shape vector for the average face of the Danes and b is the shape vector for my face, then b-a represents what makes my shape different from the averge Danes shape. So, we can add alpha(b-a) (where alpha is a positive constant) to my face shape to get an extrapolated face shape. Warping my face to this shape then produces a caricature of myself

Bells & Whistles

I changed the gender of my face my morphing with the face of an average European woman (image found here). After defining correspondence points between the two faces, I warped just my face shape to the woman’s face shape. Then, I morphed my appearance to the woman’s appearance by first warping the woman’s face shape to mine and cross-dissolving the colors. Finally, I morphed both the shape and the appearance of my face to the woman’s by morphing with warp_frac = 0.75 and dissolve_frac = 0.5